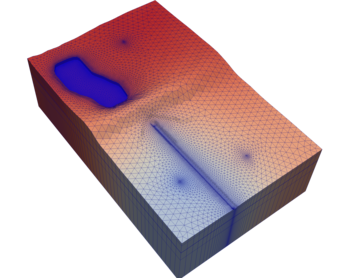
96 class(MethodSubcellTernaryType),
intent(inout) :: this
97 class(SubcellTriType),
intent(in) :: subcell
98 type(ParticleType),
pointer,
intent(inout) :: particle
99 real(DP),
intent(in) :: tmax
101 real(DP) :: dt, dtexit, texit
102 real(DP) :: t0, t, x, y, z0, z
103 integer(I4B) :: exit_face, exit_soln, event_code, i, isolv
104 type(BarycentricExitSolutionType) :: exit_z, exit_lateral
107 if (particle%iexmeth == 0)
then
110 isolv = particle%iexmeth
116 call this%find_exits(particle, subcell)
118 exit_z = this%exit_solutions(1)
119 exit_lateral = this%exit_solutions(2)
123 if (exit_z%itopbotexit == 0 .and. &
124 exit_lateral%itrifaceexit == 0)
then
130 exit_soln = this%pick_exit(particle)
131 exit_face = this%exit_solutions(exit_soln)%iboundary
132 dtexit = this%exit_solutions(exit_soln)%dt
133 if (dtexit < dzero)
then
143 call this%tracktimes%advance()
144 if (this%tracktimes%any())
then
145 do i = this%tracktimes%selection(1), this%tracktimes%selection(2)
146 t = this%tracktimes%times(i)
148 if (t > texit .or. t > tmax)
exit
150 call calculate_xyz_position(dt, &
151 exit_lateral%rxx, exit_lateral%rxy, &
152 exit_lateral%ryx, exit_lateral%ryy, &
153 exit_lateral%sxx, exit_lateral%sxy, &
154 exit_lateral%syy, exit_z%status, &
155 subcell%x0, subcell%y0, &
156 exit_z%dvdx, exit_z%v, &
157 subcell%vzbot, subcell%ztop, subcell%zbot, &
164 call this%usertime(particle)
171 if (texit .gt. tmax)
then
178 particle%advancing = .false.
187 call calculate_xyz_position(dt, &
188 exit_lateral%rxx, exit_lateral%rxy, &
189 exit_lateral%ryx, exit_lateral%ryy, &
190 exit_lateral%sxx, exit_lateral%sxy, &
191 exit_lateral%syy, exit_z%status, &
192 subcell%x0, subcell%y0, &
193 exit_z%dvdx, exit_z%v, &
194 subcell%vzbot, subcell%ztop, subcell%zbot, &
195 z0, x, y, z, exit_face)
200 particle%iboundary(level_subfeature) = exit_face
203 call this%timestep(particle)
204 else if (event_code ==
featexit)
then
205 call this%subcellexit(particle)
@, public featexit
particle exited a grid feature
@, public usertime
user-specified tracking time
@, public terminate
particle terminated
@, public timestep
time step ended
@ term_no_exits_sub
terminated in a subcell with no exit face