 |
MODFLOW 6
version 6.8.0.dev0
USGS Modular Hydrologic Model
|
 |
MODFLOW 6
version 6.8.0.dev0
USGS Modular Hydrologic Model
|
Functions/Subroutines | |
| subroutine, public | ims_odrv (n, nja, nsp, ia, ja, p, ip, isp, flag) |
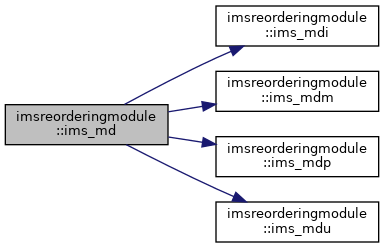
| subroutine | ims_md (n, nja, ia, ja, mmax, v, l, head, last, next, mark, flag) |
| subroutine | ims_mdi (n, nja, ia, ja, mmax, v, l, head, last, next, mark, tag, flag) |
| subroutine | ims_mdm (n, mmax, vk, tail, v, l, last, next, mark) |
| subroutine | ims_mdp (n, mmax, k, ek, tail, v, l, head, last, next, mark) |
| subroutine | ims_mdu (n, mmax, ek, dmin, v, l, head, last, next, mark) |
|
private |
Definition at line 198 of file ImsReordering.f90.

|
private |
|
private |
|
private |
|
private |
| subroutine, public imsreorderingmodule::ims_odrv | ( | integer(i4b), intent(in) | n, |
| integer(i4b), intent(in) | nja, | ||
| integer(i4b), intent(in) | nsp, | ||
| integer(i4b), dimension(n + 1), intent(in) | ia, | ||
| integer(i4b), dimension(nja), intent(in) | ja, | ||
| integer(i4b), dimension(n), intent(inout) | p, | ||
| integer(i4b), dimension(n), intent(inout) | ip, | ||
| integer(i4b), dimension(nsp), intent(inout) | isp, | ||
| integer(i4b), intent(inout) | flag | ||
| ) |
Definition at line 7 of file ImsReordering.f90.